概要

こんにちは。株式会社アイビスのTech Blog担当です。
今回は、機械学習の新しい分野として注目を浴びているNeural Radiance Fields (NeRF)についての簡単な解説と、そのNeRFの学習速度を大幅に改善した「Plenoxel」と「Instant NGP」という2つの研究成果についてご紹介したいと思います。

NeRFとは

NeRFは、UC Berkeleyの研究チームらが2020年に論文「NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis」で発表した新しい機械学習の技術です。
下図や下記動画のように、複数の視点からの画像とカメラの位置情報を入力として、対象物を含むシーンの空間内での表現を学習し、新しい視点からの画像を生成することができます。

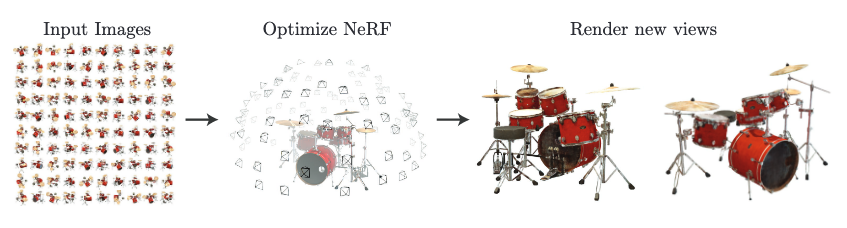
下画は、NeRFの全体像を表したものです。
NeRFで鍵となる考え方は5次元ニューラル輝度場表現とボリュームレンダリングです。

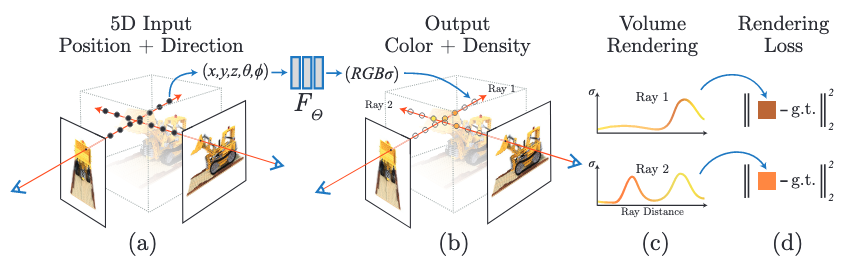
5次元ニューラル輝度場表現

NeRFでは、シーンを、三次元空間上での位置$\vec{x}= (x, y, z)$と視点方向を表す二次元ベクトル$(\theta, \phi)$を入力とし、放射される色$\vec{c} = (r, g, b)$とその位置での密度$\sigma$を出力とする関数として表現します。
これは、言い換えると3次元空間上のある点をある方向から見たときに、何色に見えるか、またその点にどのくらい物体が存在しているのかを表す関数です。
この関数は、視点方向を3次元単位ベクトル$\vec{d}$とすると以下のように表すことができます。

$$
F_{\theta} : (\vec{x}, \vec{d}) \rightarrow (\vec{c}, \sigma)
$$

今回の手法では、$F_{\theta}$として多層パーセプトロン（畳み込み層を用いない全結合層のみのニューラルネットワーク）を用いています。$\theta$は学習時に最適化すべき重みです。

上画は、今回の手法で用いた全結合ネットワークの構造をビジュアライズしたものです。
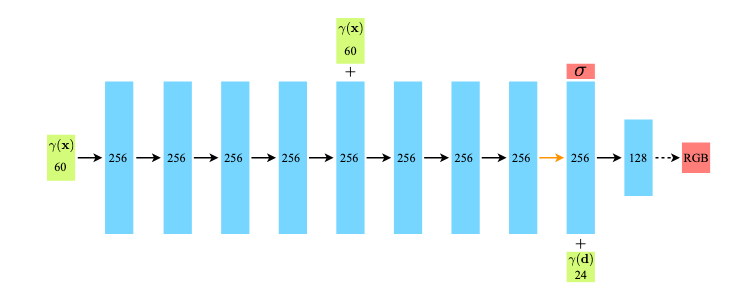
入力ベクトルは緑、中間層の出力は水色、出力ベクトルは赤のブロックで表され、ブロックの中の数字はベクトルの次元を示しています。
また、黒矢印はReLU活性化関数ありの層、オレンジ色の矢印は活性化関数無しの層、点線矢印はシグモイド関数ありの層、「+」はベクトルの結合を示しています。
図中の関数$\gamma$は入力ベクトルをより高次元の空間に変換するPositional Encoding（後述）です。
上図を見て分かる通り、関数の出力$(\vec{c}, \sigma)$のうち、$\sigma$は位置ベクトル$\vec{x}$にのみ依存し、視点方向によって変化しない値であり、視点方向を表す単位ベクトル$\vec{d}$は色情報$\vec{c}$を計算する際に使用されます。

Positional Encoding

一般的に深層ニューラルネットワークは低い周波数の関数を学習する方向に進みやすいが([2])、入力ベクトルを直接ニューラルネットワークに投入する前に、入力空間をより高い周波数を含む高次元空間に変換する関数に通すことでこれを回避し、ニューラルネットワークが高周波数の変動を学習し易くすることが可能です。
今回の手法では、この関数のことをPositional Encodingと呼んでいます。
Positional Encodingは以下のように定義されます。

$$
\gamma(p) = (sin(2^0\pi p), cos(2^0\pi p), \cdots, sin(2^{L-1}\pi p), cos(2^{L-1}\pi p))
$$

関数$\gamma$は$\mathbb{R}$から$\mathbb{R}^{2L}$への写像で、ベクトルを入力とした時はベクトルの各成分に対して個別に適用されます。
今回の手法では、位置ベクトル$\vec{x}$のエンコーディングでは$L = 10$、視点方向単位ベクトル$\vec{d}$のエンコーディングでは$L = 4$が採用されています。

ボリュームレンダリング

さて、シーンを5次元ニューラル輝度場として表現したのですが、この表現を元に実際にある視点からの画像を生成する必要があり、そこでボリュームレンダリングという手法を用います。
ボリュームレンダリングという考え方自体は、3次元的な広がりを持つデータを2次元画面に描画する方法としてすでに存在しており、今回の手法はその原則に従ったものとなります。

ある位置$\vec{x}$での密度を$\sigma(\vec{x})$、ある位置$\vec{x}$、視点方向$\vec{d}$に対応する色を$c(\vec{x}, \vec{d})$、カメラからnear平面までの距離を$t_n$、far平面までの距離を$t_f$とすると、空間中を横切るカメラレイ$\vec{r}(t) = \vec{o} + t\vec{d} \space (t_n < t < t_f)$に対応するピクセルの色$C(r)$はボリュームレンダリング法に従って以下のように計算されます。

$$
C(r) = \int^{t_f}_{t_n} T(t)\sigma(\vec{r}(t))c(\vec{r}(t), \vec{d})dt, \space where \space T(t) = \exp(- \int^{t}_{t_n} \sigma(\vec{r}(s))ds)
$$

$T(t)$はカメラレイの$t_n$から$t$に至るまでの累積透過率で、$t_n$から出発したカメラレイが粒子に衝突せずに$t$まで到達できる確率のようなものを表しています。
$t_n$と$t$の間に密度$\sigma$が大きい点が存在すると$T(t)$の値が小さくなり、$t$の位置での色が最終的なピクセルの色に反映されにくくなります。

ボリュームレンダリングの詳しい解説については以下のサイトが参考になりますので、もしよろしければご参照ください。

ボリュームレンダリング方程式1 – Computer Graphics – memoRANDOM

コンピュータ上で積分を厳密に計算することは難しいため、今回の手法では各区間においてランダムにサンプリングをする区分求積法を用いて積分値を近似的に計算しています。
まず、区間$[t_n, t_f]$をN個のビンに均等に分割します。
その後、次に一様分布に従って各ビンから1つずつ値をサンプリングします。

$$
t_i \sim \mathcal{U}[t_n + \frac{i-1}{N}(t_f-t_n), t_n+\frac{i}{N}(t_f-t_n)]
$$

$C(r)$の近似値$\hat{C}(r)$は以下のようにして求めます。

$$
\hat{C}(r) = \sum_{i=1}^N T_i(1-\exp(-\sigma_i\delta_i))c_i, \space where \space T_i = \exp(-\sum_{j=1}^{i-1}\sigma_j\delta_j)
$$

ここで、$\delta_i = t_{i+1} – t_i$です。
また、上式では、$\sigma(\vec{r}(t))dt$を$1-\exp(-\sigma_i\delta_i)$で置き換えることにより、$\alpha_i = 1-\exp(-\sigma_i\delta_i)$とした時に、上式が一般的なアルファ合成の式になるようにしています。
この多数の$(c_i,\sigma_i)$の組から$\hat{C}(r)$を求める計算は微分可能であるため、上記の手法に従って学習データとして与えられたカメラ位置から見た画像を生成し、正解画像との二乗誤差を求めれば、誤差逆伝播法を用いてニューラルネットワークの重みを更新することができます。

論文では、さらにここからHierarchical Volume Samplingという方法を用いてボリュームレンダリング時のカメラレイ上の点のサンプリング方法を効率化しているのですが、本質的では無いため、ここでは説明を省略させていただきます。

ニューラルネットワークを一切使用しないPlenoxel

さて、非常に質の高い画像を生成できるとして注目を浴びたNeRFですが、一つのシーンの学習が収束するのにGPU1枚で1~2日程度の時間がかかってしまっていました。
大規模な画像認識モデルや自然言語処理モデルの学習と比較すると、GPU1枚で1~2日の学習コストは大したことは無いのですが、2021年にUC Berkeleyの別の研究チームが論文「Plenoxels: Radiance Fields without Neural Networks」で発表した手法ではその学習時間が数分のスケールまで改善されています。
下画は、オリジナルのNeRFとPlenoxelを比較したものです。オリジナルのNeRFと比較すると100倍程度の学習速度の改善が見て取れます。

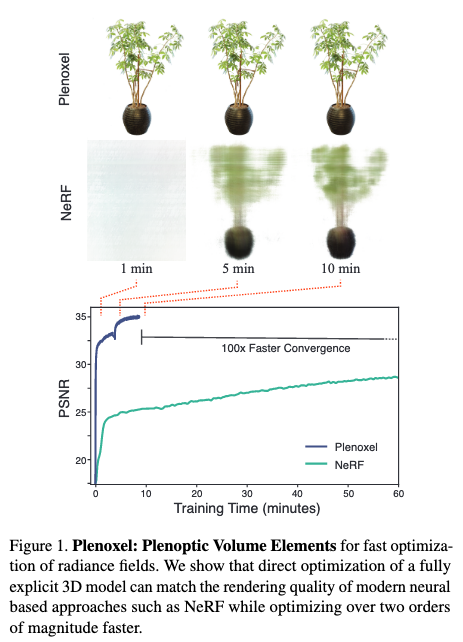
またPlenoxelは前述のオリジナルのNeRFとは異なり、ニューラルネットワークを一切用いていないという点でも特徴的です。

それでは、以下でPlenoxelの具体的な手法について詳しく見ていきたいと思います。

下画は、Plenoxelの手法の全体像を表したものです。

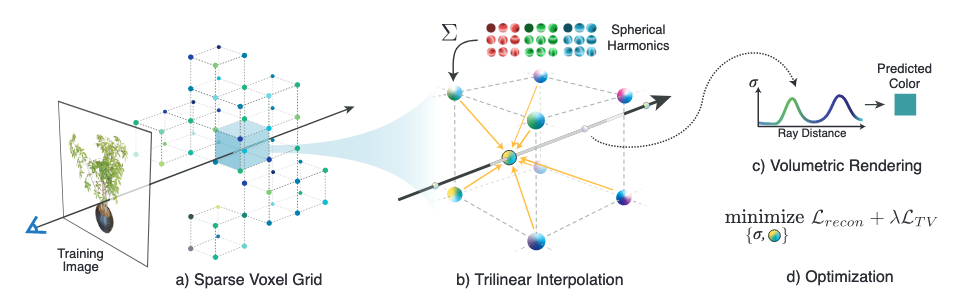
「Plenoxel」はplenopticとvoxelを組み合わせたオリジナルの造語です。
plenopticは「完全な、すべての」を意味するラテン語の”plenus”と、「見え」を意味する”optic”から来ており、空間内のあらゆる方向の光線全てを取り扱うといった意味合いで用いられるそうです。
voxelはvolumeとpixelを組み合わせた言葉で、画像が二次元配列上にpixelを敷き詰めることで表現できるのと同様に、3次元空間上のデータはvoxelを三次元配列上に敷き詰めることで表現できます。マインクラフトの世界を想像していただくと良いかと思います。

Plenoxelでは、シーンを多層ニューラルネットワークではなく、疎な三次元ボクセルグリッド上の各格子点のパラメータ群として表現しています。

球面調和関数を用いたボクセルグリッド

ボクセルグリッド上の各格子点はその点での不透明度と視点方向依存の色情報を持ちます。
不透明度はスカラー値ですが、色情報は単位球面上の連続した値であり、上手くパラメータ化する必要があります。

一般的に、1次元上の関数がフーリエ級数展開によって異なる周波数のサイン波とコサイン波の重ね合わせで表現できるのと同様に、単位球面上の関数は球面調和関数の重ね合わせで表現できます。
従って、各格子点における単位球面上の色情報は、球面調和関数の係数としてパラメータ化しています。
今回の手法では、各格子点における色情報は、2次までの球面調和関数の重ね合わせで近似するため、各色のチャネルごとに9、合計27個のパラメータで表現されることになります。

また、ボクセル内部の点での不透明度や色は、そのボクセルの8個のグリッドが持つパラメータのトライリニア補完によって計算されます。
トライリニア補完は、バイリニア補完を3次元に拡張したものです。

粗いグリッドから細かいグリッドへ

Plenoxelでは、粗いグリッドから始め、最適化し、不要なボクセルを刈り取り、残ったボクセルを各次元で半分に細分化し、最適化を続けるという方法で効率的に高解像度を実現しています。

ボクセルを刈り取るかどうかは、トレーニング時の全てのカメラレイに対して各ボクセルの最大の$T_i(1-\exp(-\sigma_i \delta_i))$がある閾値を超えていないかどうかで判断されます。

また、表面近傍の色と密度は直下のボクセルと補間されるため、トライリニア補間により、単純な刈り込みは悪影響を及ぼす可能性があります。
この問題を解決するために、ボクセル自身とその近傍のボクセルの両方が占有されていないと判断された場合にのみ、刈り込みを行うようにしています。

Plenoxelでも、学習済みのシーンの表現をもとにある視点からの画像を生成する方法は、NeRFと同様にボリュームレンダリング法を使用しています。

NeRFの学習速度をさらに改善したInstant NGP

さて、NeRFの学習速度を大幅に改善したとして大きなインパクトを与えたPlenoxelですが、Plenoxelの論文が発表されてからわずか1ヶ月後、2022年1月に今度はNvidiaの研究チームが「Instant Neural Graphics Primitives with a Multiresolution Hash Encoding」という論文を発表しました。研究チームは、この論文内でMultiresolution Hash Encodingという手法を用いてNeRFの学習を5~15秒程度にまで短縮したと主張しています。
Multiresolution Hash Encodingは、空間内に学習可能なパラメーターを埋め込むための汎用的な手法であるため、論文中ではNeRF以外にも、Gigapixel imageやSigned distance functions (SDF)、Neural radiance caching (NRC)といったタスクに応用していますが、ここではMultiresolution Hash EncodingのNeRFへの応用に絞って説明をしていきたいと思います。

Multiresolution Hash Encoding

Instant NGP (NGPはNeural Graphics Primitivesの略)と呼ばれる今回の手法は、NeRFにおけるPositional Encoding部分を、Multiresolution Hash Encodingという空間内に学習可能なパラメータを埋め込む方法に置き換えて、後続のニューラルネットワークのサイズを大幅に小さくしたものと捉えることができます。

Multiresolution Hash Encodingの目標は、ニューラルネットワーク$m(y; \Phi)$の入力$y = enc(x; \theta)$のエンコーディングについて、顕著な性能オーバーヘッドを発生させずに、近似品質と学習速度を改善することです。
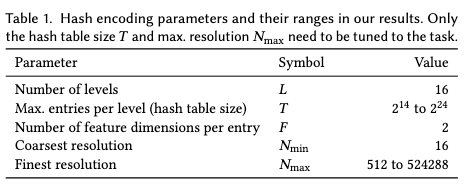
このパラメータ$\theta$は、各レベルが最大$T$個の次元数$F$の特徴ベクトルを含む、合計$L$個のレベルで構成されます。
これらのハイパーパラメータの典型的な例を下図に示します。

また、下図はMultiresolution hash Encodingの具体的な手順を表したものです。

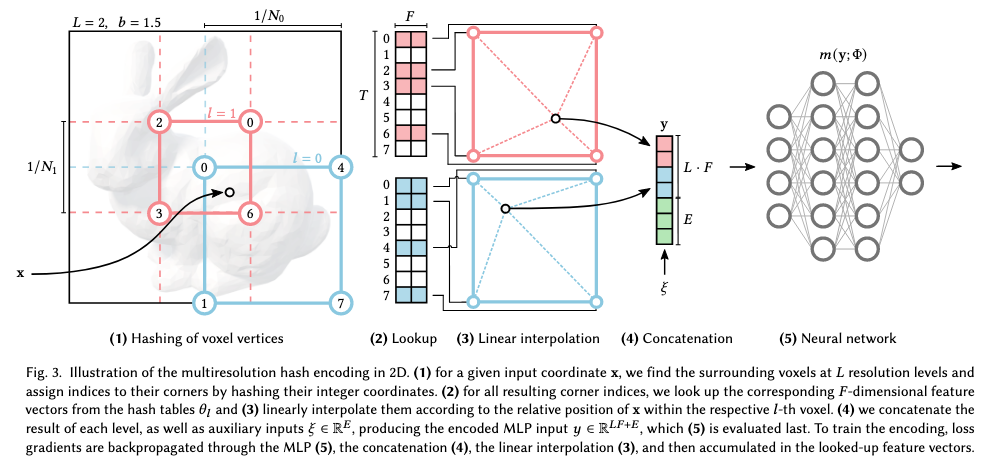
各レベル（上図では赤と青の2つ）は独立しており、概念的にはグリッドの頂点に特徴ベクトルを格納します。グリッドの解像度は、最も粗い解像度と最も細かい解像度の間$[N_{min}, N_{max}]$で、以下の等比数列によって定められます。

$$
N_l = \lfloor N_{min} * b^l \rfloor, b = \exp(\frac{\ln N_{max} – \ln N_{min}}{L-1})
$$

各レベル$l$において、0~1に正規化された入力座標$x \in \mathbb{R}^d$ (NeRFの場合は三次元なので$d = 3$)はそのレベルのグリッド解像度でスケール化されたのち切り捨て、または切り上げられます。

$$
\lfloor x_l \rfloor = \lfloor x \cdot N_l \rfloor, \lceil x_l \rceil = \lceil x \cdot N_l \rceil
$$

$\lfloor x_l \rfloor$や$\lceil x_l \rceil$はボクセルの頂点に対応します。
各ボクセルの頂点は、各レベルの特徴量ベクトル配列の要素に対応させますが、この配列は前述の通り最大でも$T$個の固定サイズです。
低解像度のレベルでは、グリッドの各頂点が保持するパラメータの総数は$T$より少ない、すなわち$(N_l+1)^d \le T$であり、このマッピングは1対1です。
より高解像度のレベルでは、ハッシュ関数$h : \mathbb{Z}^d → \mathbb{Z}_T$を使用して配列のインデックスに変換することで、特徴量ベクトル配列をボクセル空間における頂点座標をキーとしたハッシュテーブルとして扱います。
ハッシュ関数は以下の通りです。

$$
h(x) = (\oplus^d_{i=1}x_i\pi_i) \mod{T}
$$

$\oplus$はbitごとのXORを表し、$\pi_i$はここでは、$\pi_1 = 1, \pi_2 = 2654435761, \pi_3 = 805459861$が選択されています。

この時、必然的にボクセル空間内の複数の頂点が同じキーに変換され、特徴量ベクトル配列の同じ要素を指し示すという状況が発生しますが、明示的な衝突処理は行いません。

最後に、そのボクセル内での$x$の相対位置に応じて、各頂点の特徴量ベクトルで線型補完します。

これらの処理は、各レベルにおいて独立に行なわれます。各レベルにおける線型補完された特徴量ベクトルはエンコードされた視点方向などの補助的な入力$\xi \in \mathbb{R}^E$と一緒に結合され、ニューラルネットワークに投入する最終的なエンコーディング$y \in \mathbb{R}^{LF+E}$が作成されます。

ここで、このエンコーディングが、高解像度のレベルにおいてハッシュの衝突があっても、本当に上手く機能するのか疑問を持った方もいらっしゃるかと思いますが、論文では明示的な衝突処理を行わなくても良い理由として以下の2点を挙げていました。

1. 空間内の異なる2点が全てのレベルにおいて同時にキーの衝突を生じているというケースは確率的に十分低いため、後続するニューラルネットワークはあるレベルにおいてキーが衝突していたとしても、他のレベルからの情報を用いて、異なる2点を区別することができる。
2. 空間内の複数の頂点が特徴量ベクトル配列の同じエントリを指し示していたとしても、最終的なレンダリング結果に大きな影響を及ぼすのはその一部のみであり、対応する特徴量ベクトルはその一部の頂点からの勾配に支配される。従って、空間の疎な構造を自動的に取り込むことができる。

結果

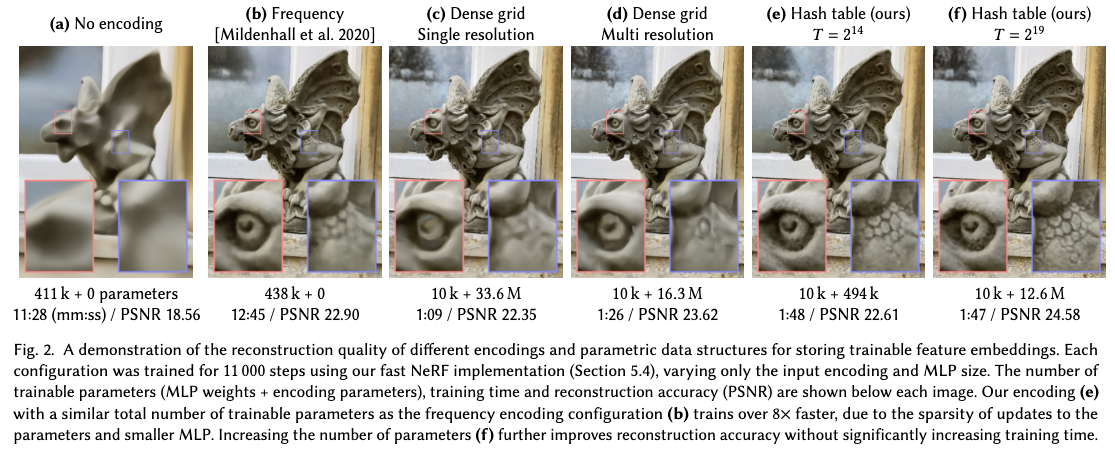
下画は先行研究との比較です。
先行研究と比較して、より少ないパラメータやより短い学習時間で、より正確な結果を生成しています。

Instant NGPの論文内で、Plenoxelとの直接的な性能比較は行われていなかったのですが、同じデータセットに対して学習をしていたので、以下にInstant NGPとPlenoxelのその学習結果を記載いたします。

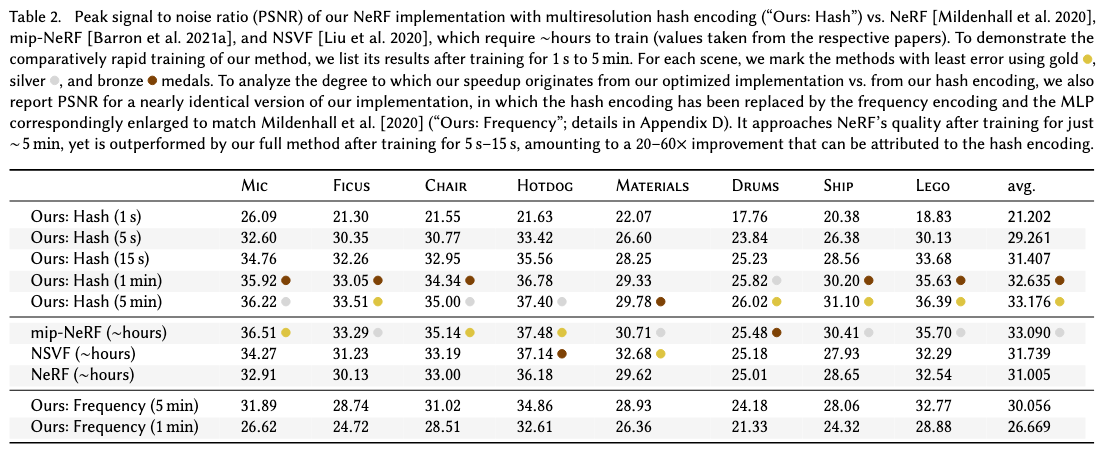
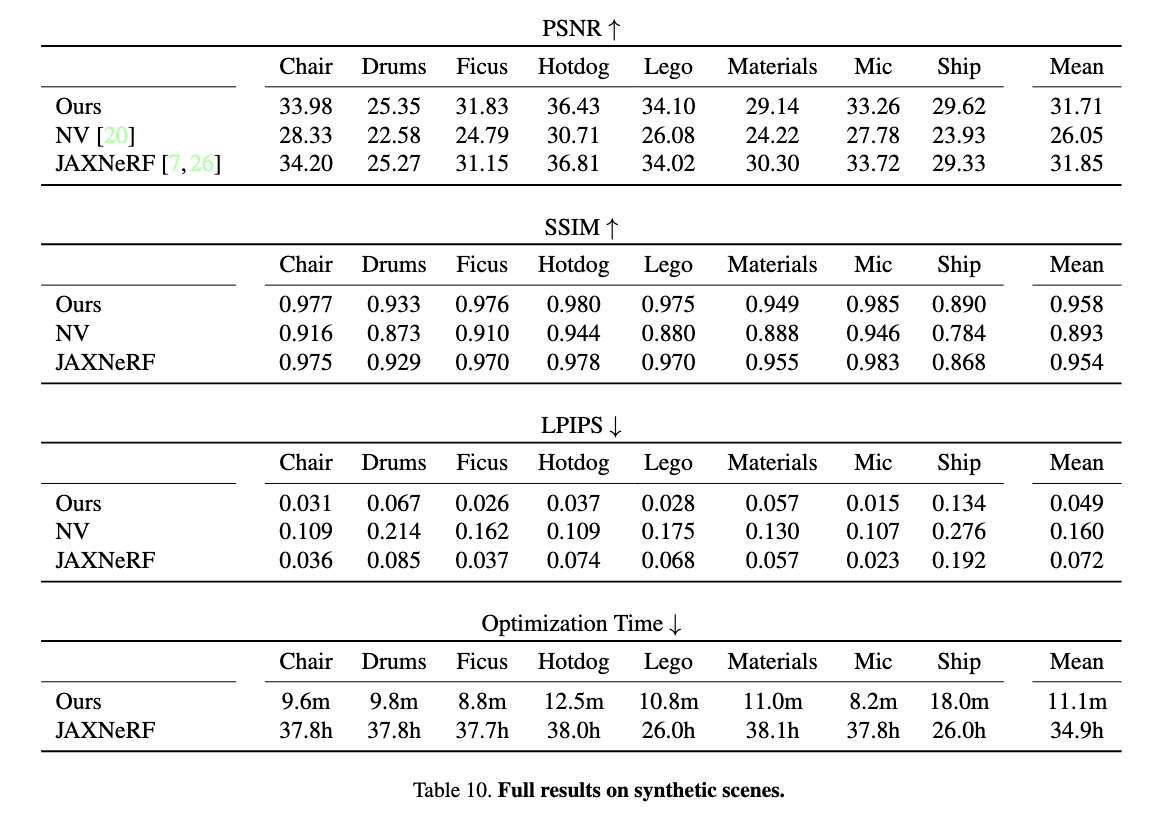
上がInstant NGP、下がPlenoxelの結果です。
Ficusや、Materials、Micといったデータセットでは、Instant NGPの15秒での結果がPlenoxelで数分学習させた結果を上回っていることが見て取れます。
このことから、Instant NGPはPlenoxelと比較しても大幅に学習速度が改善されていると言えるのではないでしょうか。

Instant NGPを試してみた

Instant NGPはこちらにソースコードが公開されていますので、NvidiaのGPU環境があれば手元でも試してみることができます。

せっかくですので、上記のソースコードを用いて、弊社の東京本社のエントランスを3次元空間上に復元してみました。

まとめ

今回は、新しい機械学習の技術として注目を浴びているNeRFについての簡単な紹介と、その学習速度を大幅に改善した「Plenoxel」と「Instant NGP」という2つの研究成果について紹介しました。

NeRFの研究は、今回紹介した学習速度を大幅に改善したものの他にも、ハイダイナミックレンジビュー合成を可能にしたNeRF in the Dark、より大規模なシーンの学習を可能にしたBlock-NeRF、NeRFで生成するシーンをテキストにより編集できるようにしたCLIP-NeRF、NeRFを動的なシーンに適用したNeural 3D Video Synthesis from Multi-view Videoなど様々な方向から取り組みが進められています。

2年前は1~2日を要した処理が、僅か2年で数秒にまで改善されるという、機械学習分野における技術革新の速さを考えると、SFやゲームの世界の話でしかなかった、現実世界をリアルタイムに取り込んでバーチャル空間に復元させたり、スマホで動画を撮るような感覚で動的な3次元空間のシーンを記録したりといった話が実現する日も、そう遠くはないのではないかと期待しています。

参考文献

1. Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, Ren Ng. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis arxiv:2003.08934
2. Nasim Rahaman, Aristide Baratin, Devansh Arpit, Felix Draxler, Min Lin, Fred A. Hamprecht, Yoshua Bengio, Aaron Courville. On the Spectral Bias of Neural Networks arxiv:1806.08734
3. ボリュームレンダリング方程式1 – Computer Graphics – memoRANDOM
4. Alex Yu, Sara Fridovich-Keil, Matthew Tancik, Qinhong Chen, Benjamin Recht, Angjoo Kanazawa. Plenoxels: Radiance Fields without Neural Networks arxiv:2112.05131
5. プレノプティックカメラ光学系を用いたマルチスペクトルイメージング
6. plenoptic 意味 – 英語 辞書 | plenoptic 日本語、定義
7. Thomas Müller, Alex Evans, Christoph Schied, Alexander Keller. Instant Neural Graphics Primitives with a Multiresolution Hash Encoding arxiv:2201.05989