概要
こんにちは。株式会社アイビスのTech Blog担当です。
今回は、論文Animating Pictures with Eulerian Motion Fieldsで提案された、水や煙のような流体の運動を含むシーンの1枚の静止画からリアルなループ動画を生成する手法を解説したいと思います。

導入
ループ動画を生成する既存の手法としては、ビデオテクスチャやシネマグラフ、ライブフォトなど様々なものがあります。これらの典型的な手法では、生成するループ動画よりも長い動画を入力とし、何かしらの動きの推定を行い、ループ動画を生成します。例えば、シネマグラフは一般的には、ビデオクリップのフレーム内の一部領域をユーザーがアニメーションまたは非アニメーション領域として指定し、アニメーションのループ動画を生成する手法のことを指します。
一方で、本手法では1枚の静止画を入力として、リアルなループ動画を自動的に生成します。本手法の対象は、流れる水やうねりのある煙などの連続的な流体運動を含むシーンです。本手法は、これらの流体の運動が、時間的に変化のない速度ベクトル場を積分することで再現できるという仮定に基づいています。流体力学等の物理学の分野において、流体を構成する各粒子それぞれの運動方程式により全体の運動記述するというアプローチをラグランジュ的記述といい、各点における流体の密度や速度ベクトルなどの場により運動を記述するというアプローチをオイラー的記述と言います。論文の様々な場所に出てくるEulerianとは、本手法においては流体の運動をオイラー的な方法で記述しようとしていることを意味しています。
本手法の概要を図2に示します。
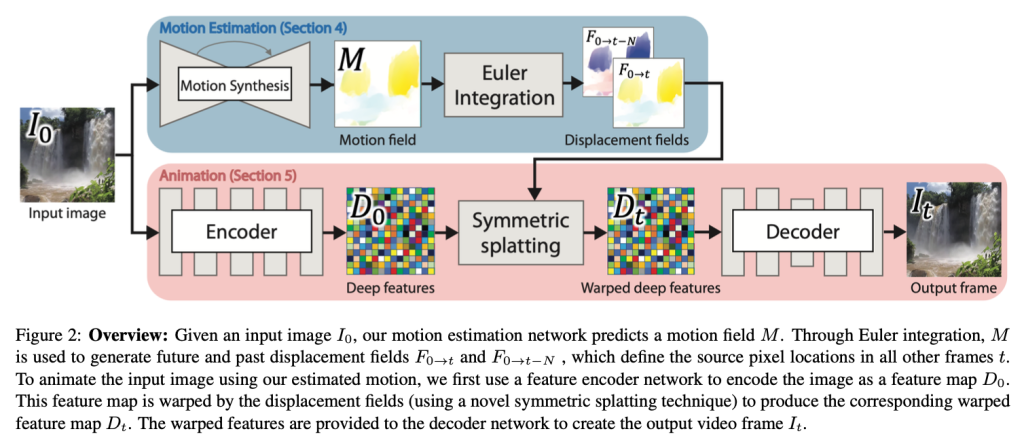
本手法では、単一の静止画$I_0$が与えられた時に、長さが$N+1$のフレーム列$I_t, t \in [0,N]$で構成されるループ動画を生成します。
本手法は、image-to-image変換ネットワークを用いて対応する速度場$M$を推定することからスタートします。この速度場$M$は、2次元平面上の位置を与えると、その位置での粒子の速度(隣接するフレーム間での動き)を返すような、時間的に不変な(すなわち、フレームtに依存しない)関数です。入力画像の各ピクセルを粒子とみなし、各フレームごとに、速度場$M$に従って少しずつ動かすことで動画を生成するというイメージです。この速度場に従って、未来のすべてのフレームにおける入力画像の各ピクセルの変位(移動量)を決定することができます。単純に入力画像の各ピクセルを速度場$M$に従って動かしただけでは隙間だらけの画像が生成されてしまうため、本手法ではDeep warpingという深層学習ベースの手法を用いて、これらの各ピクセルの変位情報から未来のフレームに対応するリアルな画像を生成します。本手法ではさらに、生成したループ動画の最初のフレームと最後のフレームが常に同じになるような工夫を施しています。
それでは、本手法の構成要素について以下で詳しく説明していきます。
動きの推定
まず初めに、速度場と速度場を推定するネットワークについて述べます。
本手法では、入力画像から速度場$M$を推定し、それを用いてループ動画の全てのフレームを生成します。速度場$M$は、時間的に不変な、全てのピクセルのその場での速度を定義するベクトルの2次元マップとなっています。従って、下式によって、あるフレームから次のフレームへの点(ピクセル)の動きをシミュレーションすることができます。
$$
\hat{X}_{t+1} = \hat{X}_t+ M(\hat{X}_t)
$$
ここで、$\hat{X}_t$はあるピクセルのフレーム$t$での座標を表します。
上式を再帰的に適用すると、将来の全てのフレーム$t$における入力画像のピクセルの位置を推定することができます。
$$
F_{0 \rightarrow t}(\hat{X}_0) = F_{0 \rightarrow t-1}(\hat{X}_0) + M(\hat{X}_0 + F_{0 \rightarrow t-1}(\hat{X}_0))
$$
$F_{0 \rightarrow t}$は各ピクセルのフレーム0とフレームtでの位置の変位場に相当します。つまり、$F_{0 \rightarrow t}(\hat{X}_0)$は、フレーム0において座標$\hat{X}_0$にあったピクセルが、速度場$M$に従って二次元平面上で流された結果、フレームtにおいてどれくらい移動したかを表しています。
動画を入力として、フレーム内の物体の位置の変位を推定する既存の手法としては、オプティカルフロー法[2]などが知られていますが、本手法では、1枚の静止画から速度場$M$を推定する必要があります。従って、画像と速度場のペアデータを用いて、入力画像$I_0$が与えられると妥当な速度場$M$を生成するような image-to-image変換ネットワークの学習を行います。ネットワーク構造の詳細は後述します。
アニメーション
続いて、推定した変位場$F_{0 \rightarrow t}$を用いて、入力画像から未来の全てのフレームにおける画像を予測し、アニメーションループを生成する方法について述べます。
Forward warping
各ピクセルの変位場に基づいて画像をワープさせる(各ピクセルを移動させる)方法として、Forward warping (Splatting)と Backward warping (Sampling)の2つが知られています。下図は、2つの手法の違いを示しています。Forward warpingでは移動元画像の各ピクセルに対して、その初期位置と変位量から移動先座標を計算し、移動先画像に割り当てます。Backward warpingでは、移動先画像の各ピクセルの位置から変位場を逆向きに辿り移動元座標を計算し、移動元画像においてリニア補完を行うことでサンプリングします。
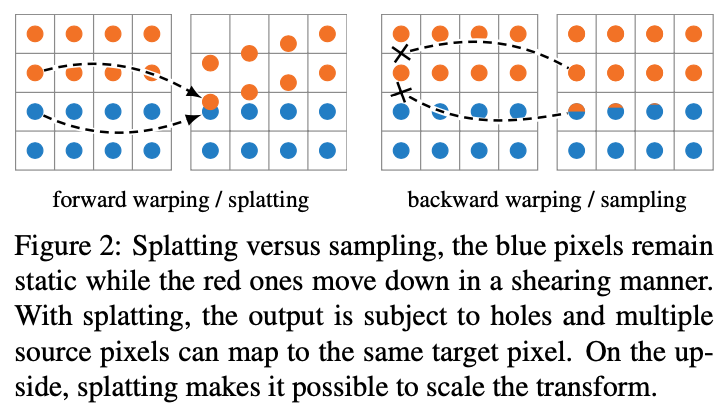
本手法では、Forward warping (Splatting)を用いて画像のワープを行いますが、Forward warpingによる画像のワープには次の2つの問題があります。
- 移動先画像において、どの入力画像のピクセルの移動先にもなっていない点、つまり穴が生成される。
- 複数の入力画像のピクセルが移動先画像において同じピクセルに割り当てられた場合に、どのように対処すれば良いのか明確ではない。
なお、Backward warpingではなくForward warpingを採用した理由については、あまり納得のいく説明がされていなかったのですが、おそらく、両者の方法を実験的に比較してみたところForward warpingの方が良い結果が得られたという理由から、本手法ではForawrd warpingを採用しているようです。
以下では、これらの問題を解決するための、深層学習ベースのDeep image warpingというアプローチを紹介します。
Deep image warping
Deep image warpingは、入力画像$I_0$と変位場$F_{0 \rightarrow t}$が与えられた時に、画像のワープによって発生する未知の領域(穴)を埋め、フレームtに対応する現実的な画像を生成するための手法です(図3参照)。

Deep image warpingは以下の3つのステップから構成されます。
- エンコーダネットワークを用いて、入力画像$I_0$を特徴量マップ$D_0$としてエンコードする。
- 推定した変位場$F_{0 \rightarrow t}$を用いて、$D_0$をForward warpingさせた特徴量マップ$D_t$を計算する。
- デコーダネットワークを用いて、ワープした特徴マップを出力画像$I_t$に変換する。
学習時において、2でForward warpingにより作成された特徴量マップ$D_t$には「穴」が空いており、3におけるデコーダネットワークは穴の空いた特徴量マップから画像を修復するように学習が行われます。これにより、推論時にもデコーダネットワークが「穴」を修復することが可能になります。
また、先ほど述べたように、Forward warpingでは複数の入力画像ピクセルが同じ移動先ピクセルに割り当てられる可能性があります。このようなピクセルにおいて、単に複数のピクセルにおける特徴量ベクトルの値を対等に平均するという方法も考えられますが、本手法ではSoftmax splattingというある種の重み付き平均をとる方法を採用し、この平均に用いる重みもエンコーダネットワークに学習させています。Softmax splattingでは、各ピクセルごとに重み係数 Z が割り当てられ、softmaxを用いて、各ピクセルの移動先画像における寄与を決定します。重み係数 Z は例えば、深度の逆数に相当すると考えられ、より距離が近いピクセルほど、移動先画像での寄与が大きくなります。
Softmax splattingを用いた、特徴量マップのワープは下式によって定義されます。
$$
D_t(\hat{X}’) = \frac{\sum_{\hat{X} \in \chi} D_0(\hat{X}) \cdot \exp(Z(\hat{X}))}{\sum_{\hat{X} \in \chi} \exp(Z(\hat{X}))}
$$
ここで、$\chi$は移動先ピクセル$\hat{X}’$に割り当てられた入力ピクセルの集合を表します。各ピクセルの重み係数$Z$は、エンコーダが生成する特徴量マップの追加のチャネルとして推定されます。
Symmetric splatting
一般的に、速度場$M$に従ったピクセルの移動を繰り返すと、ピクセルが元の位置から大きく離れ、図3に示す通り、未知の領域が大きくなります。この現象は、速度場のベクトルの向きがすべて外に向いている滝の上などの「動きの源」において特に顕著です。既に解説したように、本手法のデコーダネットワークはこれらの穴を埋めることを目的としていますが、穴が大きくなるとこのタスクが困難になってくるため、以下のような穴を小さくするための工夫を使います。
本手法では、未知の領域に有効なテクスチャ情報を提供するために、Symmetric splattingという方法を用います。この手法では、下図のように、通常の現在から未来への特徴量マップシーケンスと、速度場を反転して生成した過去から現在への特徴量マップシーケンスを、各フレームにおいて合成することで、穴の少ない、密な特徴量マップシーケンスを生成することができます。
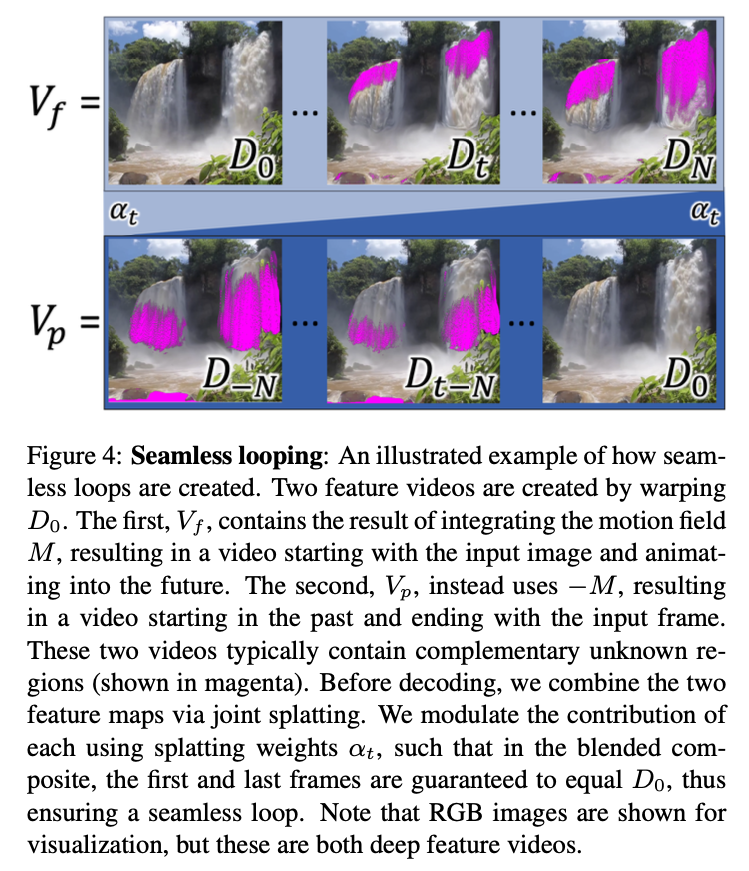
これまで説明した動画生成のプロセスでは、エンコードされた特徴マップ$D_0$を$F_{0 \rightarrow t}$でワープして未来の特徴マップシーケンス$V_f=(D_0, \dots, D_N)$を生成し、これをデコードして出力動画フレームを生成していました。しかし、速度場$M$は隣接するフレーム間の動きを定義しているので、時間軸を遡って、過去の映像を生成することができます。つまり、$D_0$を未来にワープする代わりに、$-M$を使って$F_{0 \rightarrow t}$を計算し、ワープした特徴マップシーケンス$V_p = (D_{-N}, \dots, D_0)$を生成することもできます。この特徴マップ列をデコードすると、同じようにもっともらしいアニメーションが生成されますが、主な違いは、大きな未知の領域が、$V_f$ではシーケンスの最後に発生するのに対し、$V_p$ではシーケンスの最初に発生することです。さらに、運動方向が逆になっているため、「運動源」が「運動シンク」に置き換わり、その逆もまた然りです。このため、$V_p$の未知領域の位置と、$V_f$の未知領域の位置はほぼ相補的となっています。この相補性を利用して、過去と未来の2つの特徴マップを合成することで、テクスチャ情報が欠けている領域の少ない、密な特徴マップを生成することができます(図5参照)。
Looping
ここでは、生成した動画の最初と最後のフレームが同一となり、動画が滑らかにループするための工夫について述べます。
図4からわかる通り、2つの特徴量マップ列$V_p$と$V_f$では、特徴量マップ$D_0$がシーケンスの反対側にあります。従って、最初のフレームは$V_f$の値のみ、最後のフレームは$V_p$の値のみ含むように、特徴量マップの合成におけるそれぞれの寄与が滑らかに制御できれば、動画の両端の特徴量マップおよびそれをデコードしたカラー画像は同一になることが保証され、動画は滑らかにループすることができます。そこで、下式のように、Softmax splattingに時間スケーリング係数を導入し、各シーケンスの特徴量マップの寄与度を調整します。
$$
D_t(\hat{X}’) = \frac{\sum_{\hat{X} \in \chi} \alpha_t(\hat{X}) \cdot D_0(\hat{X}) \cdot \exp(Z(\hat{X}))}{\sum_{\hat{X} \in \chi} \alpha_t(\hat{X}) \cdot \exp(Z(\hat{X}))}
$$
$\alpha_t$は時間スケーリング係数であり、下式で定義されます。
$$
\alpha_t(\hat{X}) = \left\{
\begin{array}{ll}
\frac{t}{N} & (\hat{X} \in V_p) \\
1 – \frac{t}{N} & (\hat{X} \in V_f)
\end{array}
\right.
$$
$\chi$は先ほどと同く、移動先ピクセル$\hat{X}’$に割り当てられた入力ピクセルの集合を表しますが、今回は2つの特徴量マップ由来の入力ピクセルが混ざっている可能性があります。
実装詳細
ここでは、ネットワーク構造と学習方法の詳細について説明します。
ネットワーク構造
本手法で用いる、特徴量のエンコーダ、デコーダネットワークは、SynSin[4]のアーキテクチャを用いています。SynSinは単一画像を入力として新規の視点からの画像を生成するGANベースのモデルとなっています。下図に、SynSinの概要を示します。
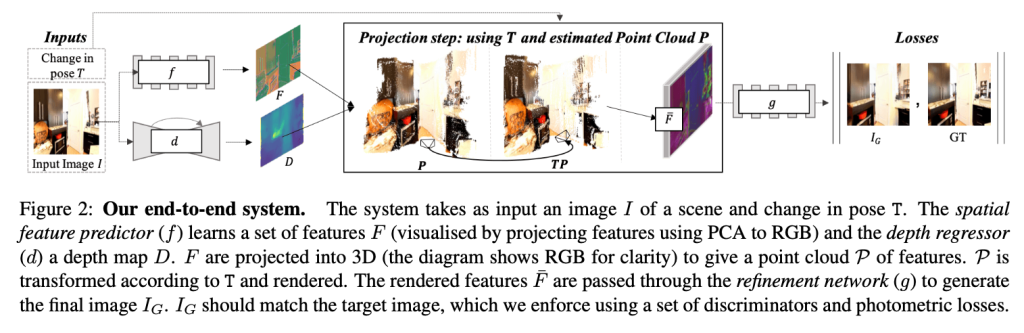
SynSinでは、上図のProjection stepにおいて、デコードした特徴量マップ$F$、推定したデプスマップ$D$、新たな視点$T$をもとに、新たな視点からの特徴量マップ$\bar{F}$を生成します。本手法では、Projection stepは先述したSoftmax splattingに、デプスマップ推定ネットワーク$d$は速度場推定ネットワークに置き換わります。
また、速度場推定ネットワークは、Pix2PixHD[5]で提案されたアーキテクチャを用いています。
学習方法
学習データとして、滝、乱流、波の流れなどの流体テクスチャを持つ自然なシーンの1196の動画を収集し、処理しています。速度場の正解データは、PWC-Net[6]と呼ばれる既存のオプティカルフロー推定器を用いて、2秒間のウィンドウにおける隣接フレーム間のオプティカルフローの平均を計算したものを使用しています。
学習時は下図のように、ビデオクリップの最初のフレーム$I_0^{GT}$と最後のフレーム$I_N^{GT}$それぞれに対してデコーダを用いて特徴量マップを作成します。$I_0^{GT}$から推定した速度場$M$を用いて、変位場$F_{0 \rightarrow t}$および$F_{0 \rightarrow t – N}$を作成し、それぞれ$D_0$と$D_N$に適用したのち、Symmetric Splattingを用いてワープされた特徴量マップ$D_t$を生成します。
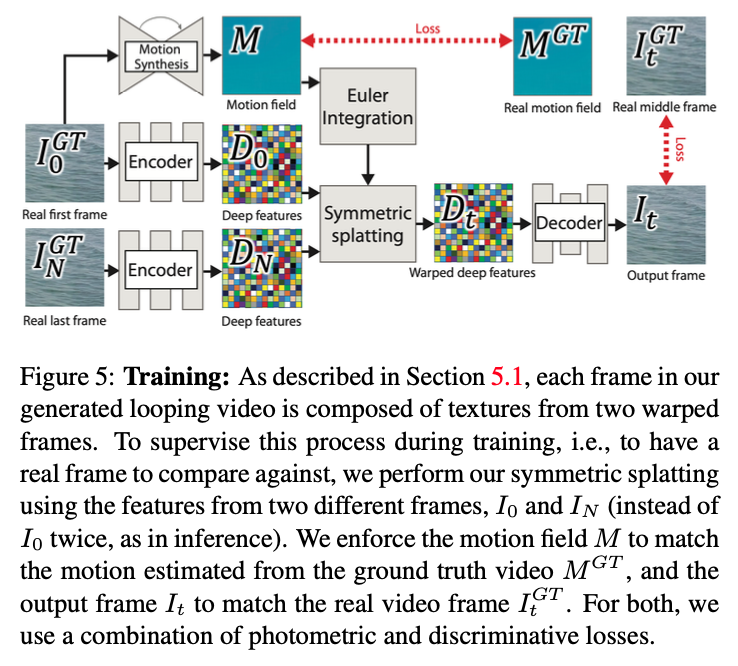
各ネットワークの学習は個別に行われます。つまり、まず初めに速度場推定ネットワークの学習が行われ、次に速度場の正解データを用いてエンコーダおよびデコーダネットワークの学習が行われます。最後に、2つのネットワークを組み合わせたend-to-endの学習が行われます。
2つのネットワークの損失関数は、どちらもL1損失関数のような計測的なロスと、Discriminatorによるロスを組み合わせたものを使用しています。
結果
本手法の解説動画および、既存研究との比較動画を以下に記載いたします。
動画を見ていただくと分かる通り、非常に注意深く観察しても、本物か生成された動画のどちらなのか判断がつかないくらい説得力のある動画を生成することに成功しています。
まとめ
今回は、水の流れや煙のような流体運動を含むシーンの1枚の静止画像から、リアルなループ動画を生成する手法を紹介しました。静止画像から動画を生成する研究としては、今回紹介したものの他にも、入力画像内の周期的な構造を自動で検出してループ動画を生成する研究[7]や、人物やキャラクターを含む静止画から3Dモデルを作成してアニメーションさせる研究[8]など様々な方向から取り組みが進められています。興味がある方はぜひそちらもご参照ください。
参考文献
- Aleksander Holynski, Brian Curless, Steven M. Seitz, Richard Szeliski. Animating Pictures with Eulerian Motion Fields arxiv:2011.15128
- OpenCVでとらえる画像の躍動、Optical Flow – Qiita
- Simon Niklaus, Feng Liu. Softmax Splatting for Video Frame Interpolation arxiv:2003.05534
- Olivia Wiles, Georgia Gkioxari, Richard Szeliski, Justin Johnson. SynSin: End-to-end View Synthesis from a Single Image arxiv:1912.08804
- Ting-Chun Wang, Ming-Yu Liu, Jun-Yan Zhu, Andrew Tao, Jan Kautz, Bryan Catanzaro. High-Resolution Image Synthesis and Semantic Manipulation with Conditional GANs arxiv:1711.11585
- Deqing Sun, Xiaodong Yang, Ming-Yu Liu, Jan Kautz. PWC-Net: CNNs for Optical Flow Using Pyramid, Warping, and Cost Volume arxiv:1709.02371
- Tavi Halperin, Hanit Hakim, Orestis Vantzos, Gershon Hochman, Netai Benaim, Lior Sassy, Michael Kupchik, Ofir Bibi, Ohad Fried. Endless Loops: Detecting and Animating Periodic Patterns in Still Images arxiv:2105.09374
- Chung-Yi Weng, Brian Curless, Ira Kemelmacher-Shlizerman. Photo Wake-Up: 3D Character Animation from a Single Photo arxiv:1812.02246