概要
論文Prescribed Generative Adversarial Networksでは、GANにおけるモード崩壊と呼ばれる問題点を解決するための手法を提案しています(著者による実装はこちらにあります)。そのキーとなるアイデアは、エントロピー正則化、すなわち、生成モデルが示す確率分布のエントロピーが大きくなるように学習を進めることです。
どのようなモデルを使用することでエントロピー正則化が可能になるのか、また、実際にどのように計算を行えば良いのかについて解説します。論文よりも詳細に計算の行間を埋めるように注意しましたので、より分かりやすくなっていると感じていただければ幸いです。
GANの復習
GAN (Generative Adversarial Network)について簡単に復習しておきます。
GANとは、画像の集合(以下、単に「データ」と呼びます)を学習し、その集合に属しているかのように見える「もっともらしい」画像を生成するためのネットワークです。
具体的には、
- 潜在変数$z$に基づいて画像$x$を生成する生成ネットワーク$x=G_\theta(z)$($\theta$はパラメータ)
および、データに含まれている画像を「本物」、生成ネットワークにより生成された画像を「偽物」と呼ぶとき、
- 与えられた画像$x$が本物である確率を出力する判別ネットワーク$D_\varphi(x)$
という2つのネットワークからなります。
学習における損失関数は、画像データの分布を$p(x)$、潜在変数$z$の事前分布を$p(z)$とするとき、
$$
\mathcal{L}(\theta, \varphi)
=
\mathbb{E}_{p(x)}\bigl[ \log D_\varphi(x) \bigr] +
\mathbb{E}_{p(z)}\bigl[ \log \bigl( 1 – D_\varphi(G_\theta(z)) \bigr) \bigr]
$$
となります。
生成ネットワークの学習では、上記の損失関数を最小化しようとします。これにより、生成ネットワークは判別ネットワークに「偽物である」と判定されにくい画像を生成するよう学習が進むことになります。
判別ネットワークの学習では、上記の損失関数を最大化しようとします。上記の関数は、本物画像と偽物画像を1:1で混ぜて作成した画像の集合について、確率モデル$D_\varphi$が正しいラベル付けを与える確率の対数、すなわち対数尤度になっています。よって、上記の損失関数を最大化することは、最尤推定を行っていることと同値であることがわかります。
モード崩壊
上記の損失関数には、一つの問題点があります。
それは、生成ネットワーク$G_\theta(z)$の出力する画像が非常に限られていて(例えば)たった一つの画像$x$という状態になっていたとしても、その画像$x$がデータの要素として「もっともらしい」限り、上記の損失は小さい値を取ってしまうことです。このように、様々なバリエーション(モード)を持つデータを使用しているにも関わらず、生成ネットワークが少数の画像のみを出力するような状態に陥ってしまうことをモード崩壊と呼びます。
モード崩壊を防ぐにはどうしたら良いでしょうか。生成ネットワークが生成する画像の分布を$p_\theta(x)$と書くことにします。確率分布に従う確率変数の「乱雑さ」を表す指標として、エントロピーが知られています。
$$ \mathcal{H}(p_\theta(x)) = – \mathbb{E}_{p_\theta(x)} \bigl[\log p_\theta(x)\bigr] $$
分布$p_\theta(x)$のエントロピーの-1倍を損失関数に加えることで、エントロピーが大きくなるように学習が進み、モード崩壊を防ぐ効果があると考えられます(エントロピー正則化)。
ただし、生成ネットワーク$G_\varphi(z)$は複雑な関数であるため、エントロピーや、その$\theta$に関する勾配を計算するのは容易なことではありません。これを可能にしたのがPrescribed GAN(以下ではPresGANと書きます)であるということになります。
PresGANのモデル
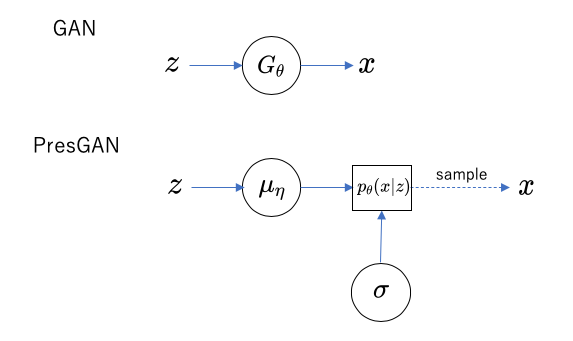
従来のGANは、事前分布$p(z)$に従う潜在変数$z$から、関数$x=G_\theta(z)$によって画像$x$の分布$p_\theta(z)$が決まると考えるものでした。
これに対し、PresGANでは、潜在変数$z$から画像$x$に関する確率分布$p_\theta(x|z)$が決まると考え、分布$p_\theta(x|z)$は以下のような形であると仮定します。
$$ p_\theta(x|z) = \mathcal{N}(\mu_\eta(z), \sigma) $$
ここで、$\mathcal{N}(\mu, \sigma)$は、$\mu$を平均とし$\sigma$を分散とする(高次元の)正規分布です。
$\mu_\eta(z)$はネットワークにより決まる関数で、パラメータ$\eta$を学習により求めることになります。分散$\sigma$も$z$の関数であると仮定するとより一般的なモデルとなりますが、学習速度向上のために分散は$z$によらず一定であると仮定し、単一の行列$\sigma$を学習により求めます(さらに、同様の理由により$\sigma$は対角行列であるとも仮定されているようです)。これらのパラメータの組$\theta = (\eta, \sigma)$が生成モデルのパラメータであり、これに判別ネットワークのパラメータ$\varphi$を加えて、PresGAN全体のパラメータとなります。
パラメータ$\theta$のもとでの$x$の分布$p_\theta(x)$は、潜在変数に関する事前分布$p(z)$を用いて
$$ p_\theta(x) = \int p_\theta(x|z) p(z) dz $$
と書くことができます。潜在変数$z$の事前分布$p(z)$は平均$0$、分散$I$(単位行列)の正規分布であると仮定されています。
エントロピー正則化項の勾配
エントロピーの定義を再掲しておきます。
$$ \mathcal{H}(p_\theta(x)) = – \mathbb{E}_{p_\theta(x)} \bigl[\log p_\theta(x)\bigr] $$
確率的勾配降下法によってエントロピー正則化(エントロピーの最大化)を行うには、勾配$\nabla_\theta \mathcal{H}(p_\theta(x)) $をなんらかの方法で推定する必要があります。エントロピーの定義式を変形してみましょう。
まず、画像$x$を分布$p_\theta(x)$からサンプリングすることは、潜在変数$z$を分布$p(z)$からサンプリングし、ベクトル$\varepsilon$を平均0、分散$I$の正規分布$p(\varepsilon)$からサンプリングした上で、$x=x(z,\varepsilon; \theta)=\mu_\eta(z) + \sigma\cdot\varepsilon$と計算することと等価です。よって、
$$
\begin{eqnarray}
\nabla_\theta \mathcal{H}(p_\theta(x)) &=& -\nabla_\theta \mathbb{E}_{p_\theta(x)} \bigl[\log p_\theta(x)\bigr] \\
&=& -\nabla_\theta \mathbb{E}_{p(\varepsilon)p(z)} \bigl[\log p_\theta(x(z, \varepsilon; \theta))\bigr] \\
&=& -\mathbb{E}_{p(\varepsilon)p(z)} \bigl[\nabla_\theta\log p_\theta(x(z, \varepsilon; \theta))\bigr]
\end{eqnarray}
$$
と書くことができます。
$\nabla_\theta$の被演算子$\log p_\theta(x(z, \varepsilon; \theta))$は、$p_\theta$と$x(z, \varepsilon; \theta)$という2つの方法で$\theta$に依存しているので、この勾配を計算する際には注意が必要です。具体的には次のように書くことができます。
$$
\begin{align}
&\nabla_\theta\log p(x(z, \varepsilon; \theta)) \\
=
&\ \Bigl.
\nabla_{\theta_1}
\log p_{\theta_1} (
x(z, \varepsilon; \theta_2)
)
\Bigr|_{\theta_1=\theta, \theta_2=\theta}
+
\Bigl.
\nabla_{\theta_2}
\log p_{\theta_1} (
x(z, \varepsilon; \theta_2)
)
\Bigr|_{\theta_1=\theta, \theta_2=\theta} \\
=
&\ \Bigl.
\nabla_{\theta}
\log p_{\theta} (x)
\Bigr|_{x=x(z, \varepsilon; \theta)}
+
\Bigl.
\nabla_x
\log p_{\theta}(x)
\Bigr|_{x=x(z, \varepsilon; \theta)}
\cdot
\nabla_\theta
x(z, \varepsilon; \theta)
\end{align}
$$
ここで、上式の第1項は期待値をとるとゼロになることが証明できます(論文では”score function identity”と書かれています)。実際、
$$
\begin{eqnarray}
\mathbb{E}_{p(\varepsilon)p(z)}
\Bigl[
\nabla_{\theta}
\log p_{\theta} (x)
\Bigr|_{x=x(z, \varepsilon; \theta)}
\Bigr]
&=&
\mathbb{E}_{p_\theta(x)}
\nabla_{\theta} \log p_{\theta} (x)
\\
&=&
\int p_\theta(x) \nabla_{\theta} \log p_{\theta} (x) dx
\\
&=&
\int p_\theta(x) \frac{\nabla_{\theta} p_{\theta} (x)}{p_\theta(x)} dx
\\
&=&
\int \nabla_{\theta} p_{\theta} (x) dx
\\
&=&
\nabla_{\theta} \int p_{\theta} (x)
\\
&=& \nabla_{\theta} 1 = 0
\end{eqnarray}
$$
となります。
ここまでの計算より、
$$
\nabla_\theta \mathcal{H}(p_\theta(x)) =
-\mathbb{E}_{p(\varepsilon)p(z)}
\bigl[
\Bigl.
\nabla_x \log p_{\theta}(x)
\Bigr|_{x=x(z, \varepsilon; \theta)}
\cdot
\nabla_\theta
x(z, \varepsilon; \theta)
\bigr]
$$
が得られました。
確率的勾配降下法でエントロピーを最大化するには、ミニバッチサイズを$B$とするとき、$b=1,\ldots,B$に対し$z_b$と$\varepsilon_b$を正規分布からサンプリングし、
$$
\nabla_\theta \mathcal{H}(p_\theta(x))
\sim
–
\frac{1}{B}
\sum_{b=1}^{B}
\Bigl.
\nabla_x \log p_{\theta}(x)
\Bigr|_{x=x(z_b, \varepsilon_b; \theta)}
\cdot
\nabla_\theta
x(z_b, \varepsilon_b; \theta)
$$
と考えてこの方向にパラメータ$\theta$を移動させる、ということを繰り返すことになります。
以下では$b$を一つ固定し、単に$z=z_b$、$\varepsilon=\varepsilon_b$と書いて、
$$
\Bigl.
\nabla_x \log p_{\theta}(x)
\Bigr|_{x=x(z, \varepsilon; \theta)}
\cdot
\nabla_\theta
x(z, \varepsilon; \theta)
$$
を計算する方法について考えます。
上式を構成する2つの勾配のうち、$\nabla_\theta x(z, \varepsilon; \theta)$の方は逆伝搬法を使って求めることができますが、もう片方の計算方法を考えるにはまだ変形が必要です。「$x=x(z, \varepsilon; \theta)$」を省略すると、
$$
\begin{eqnarray}
\nabla_x \log p_{\theta}(x)
&=&
\frac{
\nabla_x p_\theta (x)
}
{
p_{\theta}(x)
}
\\
&=&
\frac{
\int
\nabla_x p_\theta (x, z) dz
}
{
p_{\theta}(x)
}
\\
&=&
\int
\bigl( \nabla_x p_\theta (x|z) \bigr)
\frac{
p_\theta (z)
}
{
p_{\theta}(x)
}
dz
\\
&=&
\int
\bigl( \nabla_x p_\theta (x|z) \bigr)
\frac{
p_\theta (z|x)
}
{
p_\theta (x|z)
}
dz
\\
&=&
\int
\bigl(
\nabla_x \log p_\theta (x|z)
\bigr)
p_\theta (z|x)
dz
\\
&=&
\mathbb{E}_{p_\theta(z|x)}
\bigl[
\nabla_x \log p_\theta (x|z)
\bigr]
\end{eqnarray}
$$
と書くことができます($p_\theta(x,z) = p_\theta(x|z)p_\theta(z) = p_\theta(z|x)p_\theta(x)$を使っています。$p_\theta(x,z)$は$x$と$z$の同時確率分布です)。
$p_\theta(x|z)$は単なる正規分布であるため、$x$と$z$が与えられれば$\nabla_x \log p_\theta (x|z)$を計算することは容易です(正規分布の$\exp$が$\log$により外れて、$x$の2次式に関する$\nabla_x$を取るので、$x$の1次式になります)。よって、与えられた$x=x(z, \varepsilon; \theta)$における分布$p_\theta(z|x)$に従って$z$をサンプリングすることができれば、上の期待値を推定することができます。
論文では、分布$p_\theta(z|x)$から$z$をサンプリングするために、ハミルトニアンモンテカルロ法を使用しています。ハミルトニアンモンテカルロ法とは、与えられた確率分布から変数をサンプリングする手法の一種です。ある確率分布$p(x)$から$x$をサンプリングしようとする場合、このアルゴリズムで要求されるデータ(入力するデータ)は、各点$x$における$\nabla_x \log p(x)$の値であり、$p(x)$の値自体は要求されないことがポイントです。
今の状況では、与えられた$z$に対して$\nabla_z \log p_\theta(z|x)$が計算できる必要があることになります。これは、
$$
p_\theta(z|x) = \frac{
p_\theta(x|z)p(z)
}
{
p(x)
}
$$
であることを使うと、
$$
\nabla_z \log p_\theta(z|x) =
\nabla_z \log p_\theta(x|z) + \nabla_z \log p(z)
$$
となります。第2項は解析的に計算することができますし、第1項も逆伝搬法により計算することができます。
また、ハミルトニアンモンテカルロ法では、サンプリングする値(今の場合は$z$)の「初期値」を一つ与える必要があります。今の場合、サンプリングしようとしている分布$p_\theta(z|x)$を決めている$x$を生成する際に使った$z$を使用することで、ハミルトニアンモンテカルロ法の収束を早めることができます。
PresGANの損失関数
エントロピー正則化の強さを表すハイパーパラメータを$\lambda$とするとき、PresGANの損失関数は次のようになります。
$$
\mathcal{L}(\theta, \varphi)
=
\mathbb{E}_{p(x)}\bigl[ \log D_\varphi(x) \bigr] +
\mathbb{E}_{p(z)p(\varepsilon)}\bigl[
\log \bigl(
1 – D_\varphi(x(z, \varepsilon; \theta))
\bigr)
\bigr]
–
\lambda \mathcal{H}(p_\theta(x))
$$
最初の2項が従来のGANにもある敵対的損失項で、第3項がエントロピー正則化項になります。
注意点として、第2項は従来のGANに対するものから書き方が変わっていることに注意しましょう。従来のGANは生成ネットワーク$G_\theta(z)$が画像を出力する写像であったため、単に
$$
\mathbb{E}_{p(z)}\bigl[ \log \bigl( 1 – D_\varphi(G_\theta(z)) \bigr) \bigr]
$$
と書くことができていましたが、PresGANでは生成モデルが定めるのは画像$x$に関する分布であるため、その分布から画像$x$をサンプリングし、それを判別ネットワーク$D_\varphi$に見せる必要があります。そのため、ベクトル$\varepsilon$を使った
$$
\mathbb{E}_{p(z)p(\varepsilon)}\bigl[
\log \bigl(
1 – D_\varphi(x(z, \varepsilon; \theta))
\bigr)
\bigr]
$$
という書き方になっています。
PresGANの学習アルゴリズム
PresGANを学習させる際のアルゴリズムについてまとめてみます。
学習させるパラメータは$\theta=(\eta, \sigma)$と$\varphi$になります。学習における1ステップの流れは次のようになります。
- (本物画像の作成)データから画像$x_1,\ldots,x_B$を取ります($B$はミニバッチのサイズ)。また、ベクトル$\varepsilon_1,\ldots,\varepsilon_B$を正規分布$\mathcal{N}(0, I)$からサンプリングし、画像$\hat{x}_b = x_b + \sigma\cdot \varepsilon_b$を得ます。
- (偽物画像の作成)正規分布$\mathcal{N}(0, I)$から潜在変数$z_1,\ldots,z_B$およびベクトル$s_1,\ldots,s_B$をサンプリングし、画像$\tilde{x}_b = x(z_b, s_b; \theta)$を得ます。
- ($\varphi$の最適化)本物画像の集合$\{\hat{x}_b\}_b$および偽物画像の集合$\{\tilde{x}_b\}_b$を使って敵対的損失項の期待値を推定し、逆伝搬法を使って$\varphi$に関する勾配を計算し、更新します。
- ハミルトニアンモンテカルロ法を使って、各$b$に対し分布$p_\theta(z|\tilde{x}_b)$から$M$個の潜在変数$z_b^{(1)},\ldots,z_b^{(M)}$をサンプリングします。この際、サンプラーから、種々の$z$について$\nabla_z \log p_\theta(z|\tilde{x}_b) =
\nabla_z \log p_\theta(\tilde{x}_b|z) + \nabla_z \log p(z)$の値を要求されます。第1項は$\log p_\theta(\tilde{x}_b|z)$を計算して逆伝搬法を使って得られます。第2項は解析的に計算できます。また、サンプラーには初期値を渡す必要がありますが、これには$z_b$を用います。 - 各$b$に対し、4でサンプリングした潜在変数$z_b^{(1)},\ldots,z_b^{(M)}$を使って、以下の量を推定します。
- $\{(z_b, s_b)\}_b$とそこから生成された$\{\tilde{x}_b\}_b$を使って、エントロピー正則化項の勾配を推定します。最右辺の第2項は逆伝搬法で計算することができます。
- ($\theta$の最適化) $\{\tilde{x}_b\}_b$を使って敵対的損失項の第2項を推定し、逆伝搬法を使って$\theta$に関する勾配を計算します。これと6.で求めた$\nabla_\theta \mathcal{H}(p_\theta(x))$を使って$\theta$を更新します。
$$
\Bigl.
\nabla_x \log p_{\theta}(x)
\Bigr|_{x=\tilde{x}_b}
=
\Bigl.
\mathbb{E}_{p_\theta(z|x)}
\bigl[
\nabla_x \log p_\theta (x|z)
\bigr]
\Bigr|_{x=\tilde{x}_b}
\sim
-\frac{1}{M}
\sum_{m=1}^{M}
\frac{
\tilde{x}_b – \mu_\eta(z_b^{(m)})
}
{
\sigma^2
}
$$
$$
\begin{eqnarray}
\nabla_\theta \mathcal{H}(p_\theta(x)) &=&
-\mathbb{E}_{p(\varepsilon)p(z)}
\bigl[
\Bigl.
\nabla_x \log p_{\theta}(x)
\Bigr|_{x=x(z, \varepsilon; \theta)}
\cdot
\nabla_\theta
x(z, \varepsilon; \theta)
\bigr] \\
&\sim&
-\frac{1}{B}
\sum_{b=1}^{B}
\Bigl.
\nabla_x \log p_{\theta}(x)
\Bigr|_{x=\tilde{x}_b}
\cdot
\nabla_\theta
x(z_b, s_b; \theta)
\end{eqnarray}
$$
実際には、$\sigma$はあまり大きくも小さくもならないように、更新後にある範囲$[\sigma_\min, \sigma_\max]$へクランプを行っています。
論文の疑問点
ここでは、論文および著者コードを読む上で気になった点について書いておきます。
論文中の(14)式には、ミニバッチサイズ$B$が1の場合の損失関数の$\eta$に関する勾配が書かれていますが、ここに疑問点が残っています。
「PresGANの学習アルゴリズム」に書いた式において、$z_1, z_1^{(m)}, s_1$などを単に$z, z^{(m)}, s$と書くと、次のようになります(あとで論文の式と比較するため、$\tilde{x}$ではなく$x(z, s; \theta)$と書きます)。
$$
\begin{eqnarray}
\nabla_\theta \mathcal{H}(p_\theta(x))
&\sim&
–
\Bigl.
\nabla_x \log p_{\theta}(x)
\Bigr|_{x=x(z, s; \theta)}
\cdot
\nabla_\theta
x(z, s; \theta) \\
&\sim&
\frac{1}{M}
\sum_{m=1}^{M}
\frac{
x(z, s; \theta) – \mu_\eta(z^{(m)})
}
{
\sigma^2
}
\nabla_\theta
x(z, s; \theta)
\end{eqnarray}
$$
$x(z,\varepsilon; \theta)=\mu_\eta(z) + \sigma\cdot\varepsilon$であることを思い出すと、$\eta$に関する勾配は、
$$
\begin{eqnarray}
\nabla_\eta \mathcal{H}(p_\theta(x))
&\sim&
\frac{1}{M}
\sum_{m=1}^{M}
\frac{
x(z, s; \theta) – \mu_\eta(z^{(m)})
}
{
\sigma^2
}
\nabla_\eta
x(z, s; \theta) \\
&=&
\frac{1}{M}
\sum_{m=1}^{M}
\frac{
x(z, s; \theta) – \mu_\eta(z^{(m)})
}
{
\sigma^2
}
\nabla_\eta
\mu_\eta(z)
\end{eqnarray}
$$
となります。ところが、論文に書かれている式は以下のようになっています。
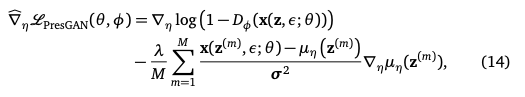
本記事での計算で得た数式で$z$となっているところのいくつかが$z^{(m)}$となっていますね($s$の代わりに$\varepsilon$と書かれているのは単なる記号法の違いからくるものです)。もちろん本記事における計算は論文の議論を元にしていますが、論文における「最終結果」の式だけこのような違いが発生しています。これについてはどういう状況かわかりませんでした(単なる書き間違いの可能性もあるとは思いますが)。
論文中の(15)式についても同様の疑問が残ります。
なお、論文著者のコードでは、本記事での計算で得た数式と同じものを実装しているように見えます。
実験
論文では、主に、
- モード崩壊が実際に緩和されていること(多くのモードが生成されること・データの分布をよく再現できていること)
- 従来のGANにエントロピー正則化を加えたことで、生成される画像の質が低下していない・改善していること
についての検証を行っています。
PresGANの特長の一つは、従来のGANにけるネットワーク構造などを引き継いだまま、エントロピー正則化項を追加することができる、という点にあります。つまり、ある生成ネットワーク$G_\theta$があるとき、これを分布$p_\theta(x|z)$の平均を与えるネットワーク$\mu_\eta$とし、これに分散パラメータ$\sigma$を追加してPresGANを構築することができます。
以下では、どのGANに基づき構築されたPresGANを使っているかがセクションにより異なるので、注意が必要です。
混合正規分布を使ったモード崩壊緩和の検証
10個の2次元正規分布を混合して作った確率分布をGANで学習させ、モード崩壊が発生するようにハイパーパラメータを調節しておきます。同じハイパーパラメータでPresGANによりこの分布を学習させると、モード崩壊が発生しないことが確認できるとのことです。

なお、この実験では「画像の分布」ではなく「2次元の点の分布」を学習するので、生成モデルの出力(あるいは出力分布の平均)は2次元であり、判別ネットワークの入力も2次元ということになります。具体的なネットワークの構成は、
We set the dimension of the latent variables z used as the input to the generators to 10. We let both the generators and the discriminators have three fully connected layers with tanh activations and 128 hidden units in each layer.
出典:Dieng, Adji B and Ruiz, Francisco JR and Blei, David M and Titsias, Michalis K. (2019). Prescribed Generative Adversarial Networks.
とのことですので、おそらく次のようなものを示しているのだと思われます。
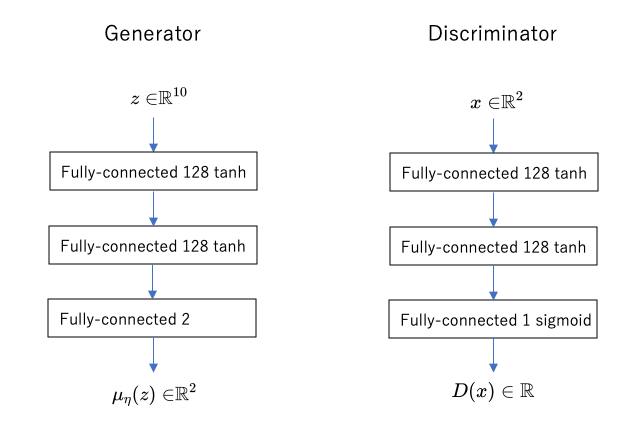
(判別モデルの最後が本当にシグモイドなのかどうか、など、論文中の説明では情報が足りず推測した部分があるため、正しさは保証できません。)
MNIST・STACKEDMNISTを使ったモード崩壊の検証
STACKEDMNISTとは、MNISTからランダムに3つの画像を取り出し、それぞれをR成分、G成分、B成分において一つの画像にするという方法で作成されたデータセットです。

MNISTに書かれている文字は10種類ですので、その分布にはモードが10個あると考えられます。同様にSTACKEDMNISTではモードが$10^3=1000$個あると考えられます。STACKEDMNISTはMNISTよりも多くのモードを持つため、モード崩壊の研究ではよく検証のために用いられているようです。
以下の表は、MNISTを様々なGANに学習させて、
- 幾つのモードを捉えられているか、すなわち、生成モデルが何種類の文字を生成するようになるか、
- 生成モデルが示す分布とMNISTの分布の間のKLダイバージェンスの値(小さい方が良いスコア。詳細後述)
をまとめたものです。
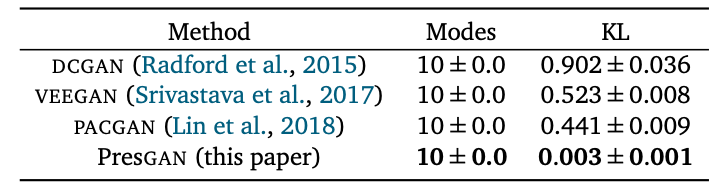
ただし、表の「KL」の意味は次のようなものとのことです。
まず、MNISTの分類器を一つ作成しておきます。この分類器は画像$x$を入力として受け取り、各数字$d\in\{0,\ldots,9\}$について、画像$x$が示す数字が$d$であるような確率$p_d(x)$を出力するようなものです。このような分類器を用意すると、画像の集合$X=\{x_i\}_{1\leq i\leq N}$が与えられたとき、ここから集合$\{0,\ldots,9\}$上の確率分布$p_X(d)$を次のように作ることができます。
$$
p_X(d) = \frac{1}{N}\sum_{i=1}^N p_d(x_i)
$$
直感的に述べれば、$p_X(d)$とは、数字$d$がその画像集合の中にどのような割合で現れるか、という分布になります。
MNISTデータセット$X$から上の方法で作られた確率分布$p_X(d)$と、それぞれのGANが生成した画像の集合$Y$から上の方法で作られた確率分布$p_Y(d)$の間の距離をKLダイバージェンスという形で測ったのが、上記の表の「KL」の列の意味になります。
モードが10個ほどしかないMNISTの場合、どのGANも全モードを捉えることができているようですが、注目するべきなのはPresGANのKLダイバージェンスの値ですね。従来のGANよりもはるかに小さい値となっていることが確認できます。
STACKEDMNISTを使った同様の実験の結果が以下の表にまとめられています。
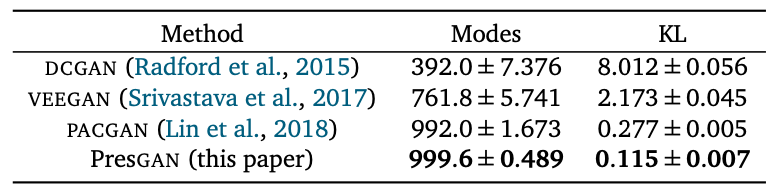
こちらでは、PresGANのみがほぼ全てのモードを捉えることができたという結果が得られています。
なお、これらの実験におけるPresGANは、DCGANを元に構築されたものとのことです。
StyleGANとPresGANの生成する画像の品質の比較
高解像度・高品質の画像を生成することで知られているStyleGANと、StyleGANを元に構築されたPresGANについて、生成された画像を比較し、画像の品質が落ちていないことを確認しています。

参考文献
- Dieng, Adji B and Ruiz, Francisco JR and Blei, David M and Titsias, Michalis K. Prescribed Generative Adversarial Networks. arXiv:1910.04302
- 著者による実装
- Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio. Generative Adversarial Networks. arXiv:1406.2661
- Alec Radford, Luke Metz, Soumith Chintala. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXiv:1511.06434
- Tero Karras, Samuli Laine, Timo Aila. A Style-Based Generator Architecture for Generative Adversarial Networks. arXiv:1812.04948