はじめに

こんにちは。株式会社アイビスのディープラーニング研究室ブログ担当です。

今回は、StyleGANの応用により低解像度の顔画像を高品質な高解像画像に変換することに成功し話題になったPULSE (Photo Upsampling via Latent Space Exploration)を使って、いくつか実験を行ってみたので、紹介します。

なお、「GANって何？」という方は、以下の記事にGANについての概説がありますので、是非お読みください。

エントロピー正則化でモード崩壊を抑制！Prescribed GANのアイデアを解説

StyleGAN

StyleGANとは、2018年に発表されたGAN（Generative Adversarial Network）であり、本物と見分けがつかない非常に高品質な画像を生成できることで知られています。
以下のようなネットワークの構造になっています。

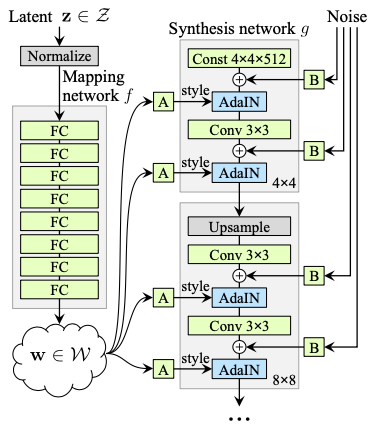
上記画像のうち、左半分のネットワークは、Mapping networkと呼ばれ、潜在変数$z\in\mathcal{Z}$を別のベクトル$w\in\mathcal{W}$に変換する全連結層からなるネットワークです（$\mathcal{Z}=\mathcal{W}=\mathbb{R}^{512}$）。
右半分のネットワークは、Synthesis networkと呼ばれ、4×4サイズの定数画像から開始し、アップサンプリングを繰り返して、最終的な出力となる1024×1024サイズの画像を生成するネットワークです。Mapping networkの出力であるベクトル$w\in\mathcal{W}$はSynthesis networkの中で18回参照されます（$(\log_2 1024 – \log_2 4 + 1)\cdot 2 = 18$）。

StyleGANの特徴の一つに、空間$\mathcal{W}$においては特徴のもつれが少ない（less entangled）というものがあります。「特徴のもつれが少ない」とは、ある画像の特徴（例えば、髪の色）に対し、$\mathcal{W}$の中に線形部分空間$L\subset\mathcal{W}$が存在し、ベクトル$w$を部分空間$L$に平行に動かすと、生成される画像のうちその特徴のみが変化する、という状況になっていることを言います（$L$が単なる部分集合ではなく線形部分空間であることが重要です）。

よって、「髪の色」という特徴に対応している線形部分空間$L\subset\mathcal{W}$を見つけることができれば、固定した$w\in\mathcal{W}$に対し、$L$に属するベクトルを色々と加える（$w + v, \ v \in L$）ことで、他の特徴を変えないまま、髪の色をいろいろと変化させることができます。

では、どうして空間$\mathcal{Z}$の方では特徴にもつれがあり、空間$\mathcal{W}$の方ではもつれが少なくなるのでしょうか。StyleGANの潜在変数$z\in\mathcal{Z}$は、学習時には正規分布$\mathcal{N}$に従ってランダムにサンプリングされます。よって、ベクトル$z\in\mathcal{Z}$における確率密度$\mathcal{N}(z)$が（例えば）小さな値のときは、潜在変数$z$に対応する画像は学習データセットの中でも珍しいタイプの画像に対応するよう、学習が進むことになります。このような縛りがあることを考慮すると、空間$\mathcal{Z}$において特徴のもつれが少なくなることはあまり期待できないように思われます。

一方、空間$\mathcal{Z}$から空間$\mathcal{W}$への写像（Mapping network）は固定された写像ではなく、学習によって決定する連続写像であるため、空間$\mathcal{W}$ではもつれが少なくなる余地が残っており、実際にそのように学習が進むとのことです。その理由については論文によると「もつれの高い表現よりも、もつれの少ない表現に基づくほうが、Synthesis networkは容易にリアルな画像を生成することができるので、もつれを小さくするような圧力があるのではないか」とのことです。

Image2StyleGAN

StyleGANは、潜在変数$z\in\mathcal{Z}$からスタートして（$w\in\mathcal{W}$を経由し）画像を生成するものです。逆に、与えられた画像に対し、それに対応する$z$や$w$を求めることができれば、ベクトルを操作することで与えられた画像の編集が可能になります。そのような問題に取り組んでいるのがImage2StyleGANです。

Mapping networkを$f\colon\mathcal{Z}\longrightarrow\mathcal{W}$とし、Synthesis networkを$g\colon\mathcal{W}\longrightarrow\mathcal{I}$とします（$\mathcal{I}=\mathbb{R}^{1024\times 1024\times 3}$は画像の空間です。また、実際には$g$にはノイズも入力するのですが、ここでは省略します）。

Synthesis networkではMapping networkの出力$f(z)$を18回参照します。学習時にはこの18回の入力にはすべて同じベクトルが与えられますが、ネットワークの構造としてはそれぞれ別のベクトルを入力しても何らかの画像を出力することは可能です。言い換えれば、$\mathcal{W}^{+}=\mathcal{W}^{18}$と定義するとき、対角写像$\delta\colon\mathcal{W}\longrightarrow\mathcal{W}^{+}; w \longmapsto (w,w,\ldots,w)$を使って、Synthesis networkを$g = g’ \circ \delta$と分解することができます（$g’\colon \mathcal{W}^+ \longrightarrow \mathcal{I}$）。

Image2StyleGANの論文では、与えられた画像$y\in\mathcal{I}$を生成するようなSynthesis networkへの入力を探索するというタスクにおいて、$\mathcal{Z}$や$\mathcal{W}$の中を探索するのではなく、$\mathcal{W}^+$の中を探索することを提案しています。つまり、$y=g(w)$となるような$w\in\mathcal{W}$はうまく見つけられない（$y=(g\circ f)(z)$なる$z$についてなら尚更）が、$y=g'(w’)$となる$w’\in\mathcal{W}^+$なら見つけられる（$y$と$g'(w’)$がかなり近くなる）とのことです。探索によって得たベクトル$w’\in\mathcal{W}^+$を操作することで、image morphing, style transfer, expression transferといった画像編集を試しています。

PULSE

さて、いよいよPULSE (Photo Upsampling via Latent Space Exploration)です。PULSEでは、StyleGANを使って顔画像の高解像度化（32×32から1024×1024等）を試みています。基本的なアイデアは、1024×1024サイズの画像を32×32サイズに縮小する写像を$d\colon\mathcal{I}\longrightarrow\mathcal{I}^\mathrm{L}=\mathbb{R}^{32\times 32\times 3}$とするとき、与えられた低解像度画像$y\in\mathcal{I}^\mathrm{L}$に対し、$y=(d\circ g’)(w’)$となるような$w’\in\mathcal{W}^+$を探索し、$g'(w’)\in\mathcal{I}$を高解像度画像として出力することです。

ここで問題となるのは、Image2StyleGANで取り組んでいたタスクと異なり、$y=d(y’)$となる画像$y’\in\mathcal{I}$は大量に存在することです（極端な話では、$y$を単に拡大することで得られたモザイク画像のような高解像度画像$y’$も$y=d(y’)$を満たします）。論文によると、$w’\in\mathcal{W}^+$であってL2誤差$|y – (d\circ g’)(w’)|^2$を最小化するだけだと、単に「ダウンスケールすると$y$になるようなある画像」が得られるだけだったそうです。よりリアルな画像を生成するため、論文では、以下のような探索の方法を提案しています。

球面上を探索する

１つ目は、球面上を探索することです。

GANでは、正規分布に基づいて生成された$z\in\mathcal{Z}$に対応する画像$(g\circ f)(z)$が学習データにまぎれていても気づかないような「リアルな画像」となるように学習を行います。よって、$y = (g\circ f)(z)$となるような$z\in\mathcal{Z}$を探索する場合、$z$の探索範囲を全空間にとるのではなく「正規分布からサンプリングされた」ことを考慮して、ある部分空間上で探索をしたほうがよい可能性があります。

ここで、$\mathcal{Z}$は$512$次元という高次元空間です。$1$次元の正規分布では原点付近がサンプリングされる確率が最も高くなりますが、高次元（$d$次元とします）正規分布に従って$z$をサンプリングした場合、$z$の原点からの距離$|z|$の値は高い確率で$\sqrt{d}$付近になることが知られています。そこで、論文では、$z\in\mathcal{Z}$の代わりに、半径$\sqrt{512}$の球面$S$上で探索することを提案しています。

以上は一般のGANで成立する話ですが、StyleGANでは、$\mathcal{W}$ではなく$\mathcal{W}^+$の上で探索を行ったほうが良い、つまりSynthesis networkの18個の$w$の参照に別々の値を入力する余地を残して探索したほうが良い、という知見もあります。これを考慮すると、$S^+ = S^{18}$の上で探索を行うのがよいと考えられます。

よって、$(z_1,\ldots,z_{18})\in S^+$をとり、$w’=\bigl(f(z_1),\ldots,f(z_{18})\bigr) \in \mathcal{W}^+$、$y’=g'(w’)$のように計算して、ロス$|y-d(y’)|^2$に関する勾配逆伝搬を行い、各$z_i$を（$S$に沿った方向へ）更新する、ということをやれば良いのか？というのがここまで読んだときの私の理解だったのですが、実際のところはMapping network $f$そのものではなく、$f$を近似するように（？）調節したより単純な関数を使っているようです。ここでどうして$f$をそのまま使わないのかについては、論文を読んでも理解することができませんでした（高速化のため？）。

Cross Loss

もう一つは、探索（最適化）におけるロスにCross Lossを加えるというものです。

Image2StyleGANでそうだったように、$S$の中を探索するのは生成できる画像の幅を狭めすぎてしまうため、より広い空間である$S^+$の中を探索しようとしています。ここで「より広い」と述べましたが、$S$は$S^+$の中に対角写像$\delta\colon S\longrightarrow S^+; z \longmapsto (z,\ldots,z)$で埋め込まれていると見なしています。

しかし、学習時にはStyleGANへ入力されるのは$\delta(S) \subset S^+$の点のみであるため、$S^+$の中を探索するといっても、$\delta(S)$から離れすぎてしまうのはリアルでない画像を生成してしまうことに繋がると考えられます。そこで、$\delta(S) \subset S^+$において値が小さくなるような関数をロスに加える、というのがCross Lossの考え方です。具体的には、$u, v \in S$に対し$u$と$v$のなす角を$\theta(u,v)$とするとき、$(z_1,\ldots,z_{18})\in S^{+}$に対し、

$$ GEOCROSS(z_1,\ldots,z_{18}) = \sum_{i<j} \theta(z_i, z_j)^2 $$

を加えます。

PULSEで髪の色を指定して遊ぶ

Image2StyleGANが取り組んでいるのは、高解像度な画像を与えられたとき、言い換えれば、1024×1024個のピクセルの色がすべて指定されたときに、その画像を生成するような$\mathcal{W}^+$のベクトルを見つけるというタスクでした。一方、PULSEでは「32×32に縮小したときの各ピクセルの色」という、1024×1024のサイズの画像にとってはかなり緩い条件を与えられた際に、その条件を満たす画像（たくさんある）のうち顔画像としてもっともらしいものを見つける、というタスクをこなしています。

PULSEのアルゴリズムは汎用的であって、ロス関数を書き換えることで、この「緩い条件」の部分を変更することができます。そこで「（32×32に縮小した後に）特定の領域の色だけを指定する」という条件に変えてみることを考えました。これはPULSEの公式実装（40cacb9）において、参照画像(ref_im)として（RGB画像ではなく）RGBA画像を入力できるようにし、単純なL2ロスの代わりに、参照画像のアルファ値で重みづけたL2ロスを使うようにすることで実現できます。

この状態で、左のような画像を入力してみたところ、右のような出力が得られました。

（左の画像の黒い部分は実際には透明です。）

一応頭の付近が青になってはいるのですが、肌の色も含めて全体的に青くなってしまっており、髪が青色というよりは、写真を撮ったあとに全体的に青色にするフィルターを通したかのような印象です。そこで、肌の色も指定するようにします。ついでに、髪の色を変化させたときに比較しやすいように背景の色も指定しておきます。

（左肩のあたりに緑色のアーティファクトが出ていますが、）一応、青く髪を染めた人に見えるとは思います。ただ、影まで青かったりする点はやはりイマイチですね。

(金髪)-(黒髪)を計算する

ベクトル$w\in\mathcal{W}^+$が黒髪の顔画像を表しているとします。ベクトル$v\in\mathcal{W}^+$であって、$w+v$が（同じ人物の）金髪の顔画像になるようなものを見つけたい、ということを考えます。

欲しいのは、同一人物の同じ構図の画像であって、黒髪のバージョンのものと、金髪のバージョンのものです。もし実際の写真であってそのようなものが得られたら、これらの画像からImage2StyleGANによってベクトル$v_1, v_2 \in \mathcal{W}^+$を計算し、$v = v_2-v_1$とすれば良いはずですが、そのような写真が容易に得られるわけではありません。

一方で、上で小改変したPULSEを使えば、髪（頭付近）の色を指定し、その他のパラメータは指定しないで（ランダムに選んで）画像を生成することができます。そこで、乱数シードを固定しておけば、上記の「同一人物の同じ構図の画像であって、黒髪のバージョンのものと、金髪のバージョンのもの」が得られるかもしれないと思い、試してみました。

一番気になるのは、髪の長さが変わってしまうことでしょうか。また、眉も薄くなってしまっている、肌の汚れが消えている、全体的に明るくなっているように見える、というのも気になります。しかし、目や鼻の形、皺の入っている場所などはよく似た画像を得ることはできました。

これら2枚の画像の生成に用いられた$\mathcal{W}^+$の2つのベクトルの差$v$を計算しました。次に、PULSEを使って様々な黒髪の顔画像を生成し、その生成途中に用いられたベクトル$w\in\mathcal{W}^+$に$v$を加えて生成した画像と並べてみます。

何より目立つのは、男性が女性になってしまうケースがあることですね。加えて、やはり、髪型が変わる、肌の汚れが消える、全体的に明るくなる、などの「意図しない変化」は発生してしまっています。しかし、目や鼻の形を保つことは出来ているように見えます（表情は微笑む方向に変わっているようです）。

今回は、変換前となっている黒髪画像は、PULSEがある32×32の画像の高解像度化として出力したものであり、実在の人物ではありません。実在する黒髪の人物の顔画像を入力して金髪化する場合は、Image2StyleGANを使って$w\in\mathcal{W}^+$を得て、それに上記のベクトル$v$を加えれば良いと思われます。

まとめ

1. StyleGANの空間$\mathcal{W}$は、特徴のもつれが少ない（less entangled）という性質がある。
2. 出力画像$y$について条件が与えられ、その条件を満たす画像を生成するベクトル$w\in\mathcal{W}^+$を探索する研究として、Image2StyleGANやPULSEがある。
3. PULSEを利用すると、指定した髪色の顔画像を生成したり、「黒髪を金髪に変換するベクトル$v\in\mathcal{W}^+$」（である程度の精度のもの）を生成することができた。

参考文献

1. Sachit Menon, Alexandru Damian, Shijia Hu, Nikhil Ravi, Cynthia Rudin. PULSE: Self-Supervised Photo Upsampling via Latent Space Exploration of Generative Models. arXiv:2003.03808
2. adamian98/pulse
3. Tero Karras, Samuli Laine, Timo Aila. A Style-Based Generator Architecture for Generative Adversarial Networks. arXiv:1812.04948
4. Rameen Abdal, Yipeng Qin, Peter Wonka. Image2StyleGAN: How to Embed Images Into the StyleGAN Latent Space? arXiv:1904.03189